VC Dimension
VC dimension (for Vapnik–Chervonenkis dimension)
The VC dimension of non-linear classifier is difficult to calculate, however the VC dimension of a linear classifier is easier to calculate.
Before explaining the VC dimension, lets first understand the related basic concepts. We start with the general position of points. According to wiki "A set of at least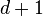 points in
points in 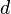 -dimensional space is said to be in general linear position(or just general position) if no hyperplane contains more than
-dimensional space is said to be in general linear position(or just general position) if no hyperplane contains more than 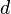 points. In more generality, a set containing
points. In more generality, a set containing  points, for arbitrary
points, for arbitrary  , is in general linear position if and only if no
, is in general linear position if and only if no  -dimensional flat contains all
-dimensional flat contains all  points"
points"
The concepts of general points is illustrated in fig-1 and fig-2 below:
Now we explain another important concept called shattering of points. A hypothesis h ∈ H is said to shatter n points in m dimensional space, if it can correctly classify all possible combination of n points in m dimensional space.
Line:
For the case of the linear classifier, let's say we have 3 points in 2D space. The 3 points can take either class A (-) or class B (+) which gives us 23 (=8) possible combinations (or learning problems). We can see in fig-3 (a) that a line can shatter 3 points (in general position). (we can easily check the case of 1 and 2 points). Now, for the case of 4 points, we can have maximum of 24 (=16) possible combinations. We can see in fig-3 (b), that the line was unable to shatter the two classes. So, we can say that the line can shatter at most 3 points.
Definition1: The basic definition of VC dimension is the capacity of a classification algorithm and is defined as the maximum cardinality of the points that the algorithm is able to shatter.
Definition1: The Vapnik-Chervonekis dimension, VC(H), of hypothesis space H defined over instance space X is the size of the largest finite subset of X shattered by H. If arbitrarily large finite sets of X can be shattered by H, then VC(H) ≡ ∞. For any finite H, VC(H) ≤ log2|H|. To see this, suppose that VC(H) = d. Then H will require 2d distinct hypotheses to shatter d instances. Hence, 2d ≤ |H|, and d = VC(H) ≤ log2|H|."
Hence we can see that the VC dimension of a line in 2D space is 3.
Similarly, we can define the VC dimension of rectangles and squares.
Rectangle:
The rectangles can shatter 4 points but not 5 points. Hence, the VC dimension of rectangle is 4. Fig-4 illustrates the shattering of points by a rectangle.
The minimum enclosing rectangle that allows us to select all five points is defined by only four points – one for each edge. So, it is clear that the fifth point must lie either on an edge or on the inside of the rectangle.
Square:
The square can shatter 3 points but not 4 points. Hence, the VC dimension of a a square is 3. Fig -5 illustrates the shattering of points by a square.
In fig-5 (a), we can see that the square can shatter 3 points easily.
Now, let's take the case that the 4 points are laid out to form the four edges of a rectangle. Let us suppose, we want to select the points A and C. So, whenever we attempt to select A and C, either we miss one of them or we include the points B or D (which we assume to be of different class than A and C). Fig -5 (b) illustrates this case. Hence, we can say that the VC dimension of a square is 3.
Rotatable rectangles:
Rotatable rectangles are VC dimension 7. Suppose we have a regular heptagon. It’s easy to get any subset of 0, 1, 2, 6, or 7 points. For 3 points, all configurations are symmetric to ABC, ABD, ABE, or ACE. The figure below shows how can we can rotate rectangles to capture these 3 point configurations.
Similarly, we can capture the 4 point configurations.
Intervals on Real Line:
Suppose we want to shatter the real line with intervals. One interval gives us VC dimension 2.
Pairs of intervals give us VC dimension 4.
More concepts on VC dimension can be found in the following references:
References:
VC dimension (for Vapnik–Chervonenkis dimension)
The VC dimension of non-linear classifier is difficult to calculate, however the VC dimension of a linear classifier is easier to calculate.
Before explaining the VC dimension, lets first understand the related basic concepts. We start with the general position of points. According to wiki "A set of at least
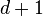 points in
points in 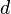 -dimensional space is said to be in general linear position(or just general position) if no hyperplane contains more than
-dimensional space is said to be in general linear position(or just general position) if no hyperplane contains more than 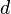 points. In more generality, a set containing
points. In more generality, a set containing  points, for arbitrary
points, for arbitrary  , is in general linear position if and only if no
, is in general linear position if and only if no  -dimensional flat contains all
-dimensional flat contains all  points"
points"The concepts of general points is illustrated in fig-1 and fig-2 below:
Line:
For the case of the linear classifier, let's say we have 3 points in 2D space. The 3 points can take either class A (-) or class B (+) which gives us 23 (=8) possible combinations (or learning problems). We can see in fig-3 (a) that a line can shatter 3 points (in general position). (we can easily check the case of 1 and 2 points). Now, for the case of 4 points, we can have maximum of 24 (=16) possible combinations. We can see in fig-3 (b), that the line was unable to shatter the two classes. So, we can say that the line can shatter at most 3 points.
Definition1: The Vapnik-Chervonekis dimension, VC(H), of hypothesis space H defined over instance space X is the size of the largest finite subset of X shattered by H. If arbitrarily large finite sets of X can be shattered by H, then VC(H) ≡ ∞. For any finite H, VC(H) ≤ log2|H|. To see this, suppose that VC(H) = d. Then H will require 2d distinct hypotheses to shatter d instances. Hence, 2d ≤ |H|, and d = VC(H) ≤ log2|H|."
Hence we can see that the VC dimension of a line in 2D space is 3.
Similarly, we can define the VC dimension of rectangles and squares.
Rectangle:
The rectangles can shatter 4 points but not 5 points. Hence, the VC dimension of rectangle is 4. Fig-4 illustrates the shattering of points by a rectangle.
The minimum enclosing rectangle that allows us to select all five points is defined by only four points – one for each edge. So, it is clear that the fifth point must lie either on an edge or on the inside of the rectangle.
Square:
The square can shatter 3 points but not 4 points. Hence, the VC dimension of a a square is 3. Fig -5 illustrates the shattering of points by a square.
In fig-5 (a), we can see that the square can shatter 3 points easily.
Now, let's take the case that the 4 points are laid out to form the four edges of a rectangle. Let us suppose, we want to select the points A and C. So, whenever we attempt to select A and C, either we miss one of them or we include the points B or D (which we assume to be of different class than A and C). Fig -5 (b) illustrates this case. Hence, we can say that the VC dimension of a square is 3.
Rotatable rectangles:
Rotatable rectangles are VC dimension 7. Suppose we have a regular heptagon. It’s easy to get any subset of 0, 1, 2, 6, or 7 points. For 3 points, all configurations are symmetric to ABC, ABD, ABE, or ACE. The figure below shows how can we can rotate rectangles to capture these 3 point configurations.
Similarly, we can capture the 4 point configurations.
Intervals on Real Line:
Suppose we want to shatter the real line with intervals. One interval gives us VC dimension 2.
Pairs of intervals give us VC dimension 4.
More concepts on VC dimension can be found in the following references:
References:







No comments:
Post a Comment