Balanced Binary Tree LeetCode

Problem: Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

 Example 1:

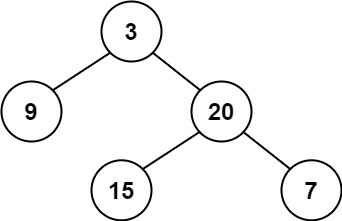
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

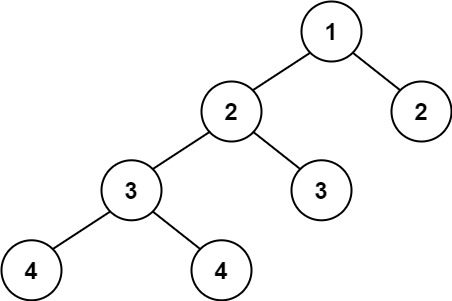
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• -104 <= Node.val <= 104

This problem is popular in LeetCode. A collection of hundreds of interview questions and solutions are available in our blog at Interview Question

Solution